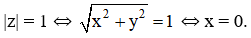Bài 5 (trang 134 SGK Giải tích 12): Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn từng điều kiện:

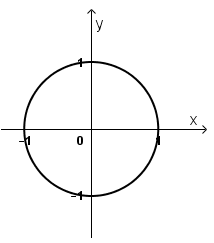
a) |z| = 1

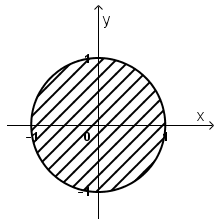
b) |z| ≤ 1

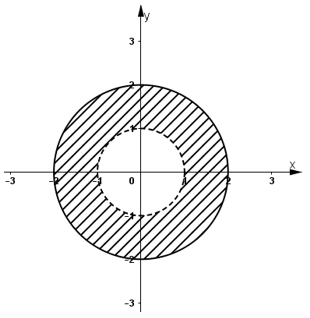
c) 1<|z| ≤ 2

d) |z| = 1 và phần ảo của z = 1

Bài giải:

Gọi số phức z = x + y.i có điểm biểu diễn là M(x; y).

a) |z| = 1 ⇔ √(x² + y² ) = 1 ⇔ x² + y² = 1

Vậy tập hợp điểm M là đường tròn tâm O(0; 0), bán kính R = 1.

b) |z| ≤ 1 ⇔ √(x² + y² ) ≤ 1 ⇔ x² + y² ≤ 1

Vậy tập hợp điểm M là hình tròn tâm O(0; 0), bán kính R = 1.

c) 1 < |z| ≤ 2 ⇔ 1 < √(x² + y² ) ≤ 2 ⇔ 1 < x² + y² ≤ 4.

Vậy tập hợp điểm M là hình vành khăn tâm O, bán kính đường tròn nhỏ bằng 1,đường tròn lớn bằng 2, không kể các điểm thuộc đường tròn nhỏ.

d) Phần ảo của z bằng 1 ⇔ y = 1

Vậy điểm M(0; 1).